Confrontational reactions I consider to be some special types of reactions, in which an action of a given entity $p$, and reaction of an entity $q$ to it share the same referent entity $r$.
For example, such a confrontational reaction to an action $e_1 e_2 e_3 +$ (possibly interpreted as “$e_1$ moving/attracting $e_2$ to $e_3$”), could be a reaction $e_3 e_2 e_3 -$ (possibly meaning “$e_3$ repels $e_2$ from $e_3$”). Another example of such a reaction would be $e_2 e_2 e_3 -$ (for example: “$e_2$ goes away from $e_3$”). In both actions, an entity $e_3$ (referent entity) occurs as a referent.
This kind of reaction is some kind of “entering a game of forces” by an entity with other one, in which those two entities try to manipulate with some entity.
- $a, b, c, d$ – real number, such that: $|b| < |a|$
- $p, q$ – two (hypothetically also the same) entities
- $A$ – a choice of action
- $\vec{}$ – vector
- $\hat{}$ – unit vector
- $\vec{pAq}$ – action $A$ of $p$ on $q$
Also, $int_1$ is an action, and $int_2$ – a reaction of confrontation
Action
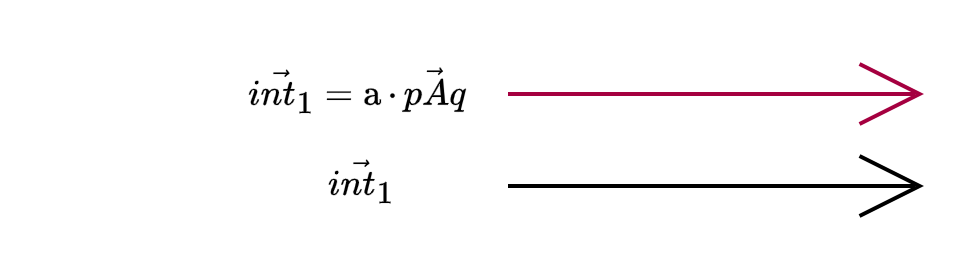
Opposition, counteraction – reaction opposing direction of the initial action
Some other possible names: dissensus, disagreement
Reversion, underpower – initial action vector with a larger magnitude, than the reaction vector to it

Equalisation, impasse – reaction of neutralisation of the impact of the initial action

Inversion, overpower – reaction stronger than the initial action

Imitation, coaction – reaction, with the same direction, as the initial action vector
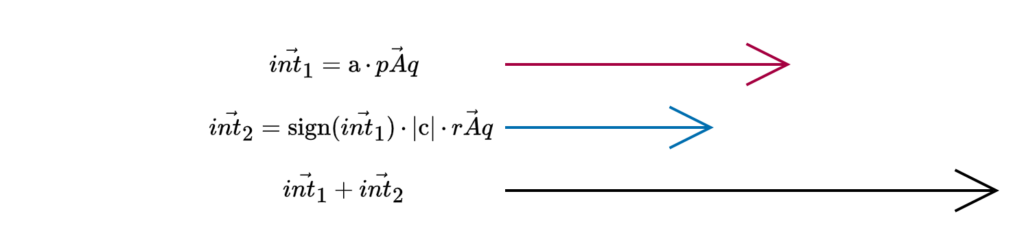
Some other possible names: consensus, agreement
Passivity – lack of reaction
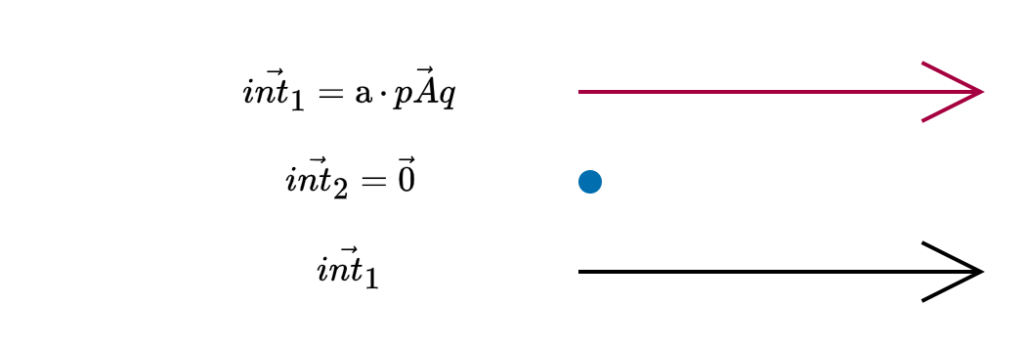
The notation can appear ambiguous, and the very $sign$ function can appear confusing. The idea to treat “signs” of vectors (sense of vectors laying on the same line) this way may appear interesting, but I’ll rather change it in the future for clarity.
What important remains to be explained, is the meaning of a notation $\vec{xAy}$. I’d like to try to explain it in one of the future posts.
Possible results of the reaction of confrontation
There appears to be three possible reasults of reaction of confrontation, in terms of the difference of the directions of the two interactions.
The terms I used somewhat resemble the musical naming. If you’d have some suggestions of other names for them, you can write them in the comments.
Consonance – action and reaction of confrontation having the same direction

Cancellation, status quo – action and reaction of confrontation cancelling each other

One of the interactions is a zero vector in this case.
Dissonance – action and reaction of confrontation having opposite directions

The reaction vectors in these set of interactions could then be called consonant, cancelling and dissonant.
Few interesting classes and relations could be distinguished this way.
For example:
Inversion is a special type of dissonance
Both reversion and imitiation are special types of consonance
Etc.
The two possible ways, in which an entity can react are the same as above: coaction or counteraction.
Some simple notation
Eventually, one could use a simple notation, to denote these types of reactions, with the first term denoting the efforts or attitude of the reacting entity, and the second term, the outcome of that reaction, in terms of its impact on the initial action.
Then:
- $+,+$ (following direction, direction (of action) preserved) – imitation
- $0,+$ (not performing a reaction, direction preserved) – passivity
- $-,+$ (opposing the action, direction preserved) – reversion
- $-,0$ (opposing the action, lack of direction) – equalisation
- $-,-$ (opposing the action, direction inversed) – inversion
One could also add some braces for use with some other notation, if needed.
For results of efforts of the acting entity, one could for example simply write $+$, $0$, or $-$ signs, to denote the (at least partial) fulfillment of intended impact, its neutralisation, or a result opposite to the intention of the agent of action.
To complete the list of possible cases, we can also consider the amplification or degree, to which an initial action was altered (here, vector’s sense and magnitude only) – alteration, by setting + to denote the boost or enhancement (of impact) of that action, 0, a lack of its change or its passing in the unchanged form, and -, its reduction.
I may yet mention this in some future article, more related about the very actions.
Relationship to astrological modalities
I wonder, if astrological modalities of Caridnal, Fixed and Mutable can be defined this way.
- Cardinal modality, as initiation or pioneering could probably be thought of as an action
- Mutable modality, as flowing with environment or adaptability seems to be related with imitation, and perhaps also a passivity
- Fixed modality, as preservation or resisting change appears to be related with the inversion
Thanks for your time reading, and I hope it was inspiring or interesting for you